FunctionsInverse Functions
Team sports is a world of split-second decisions and fast-moving bodies. Teammates choose where to place a pass. Referees decide who gains possession of the ball. Fans follow the action from great distances. In all these cases, jersey colour is deciding factor in how these instantaneous decisions are made.
Let's take a look at the the Balligon Soccer League. Match each team to a jersey colour such that you have a
Recall that the team mascots make up the
while jersey colours make up the range. In function notation, we write this relationship as f(
Take a look at the end of season tournament brackets.
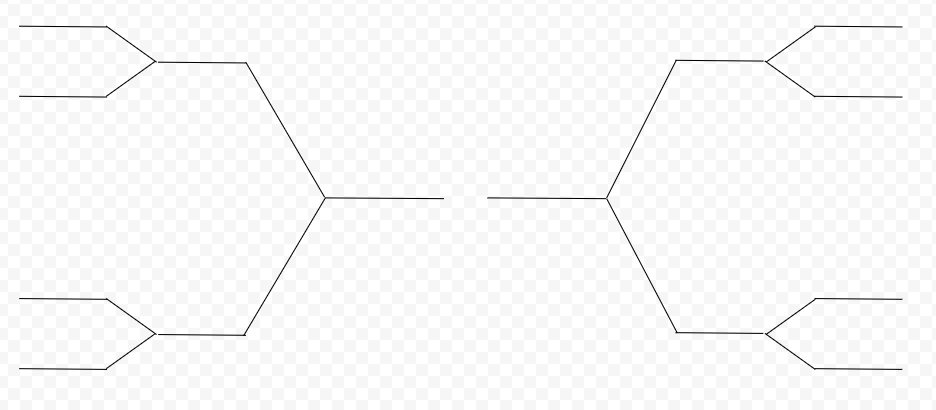
Example brackets. Fill in with teams matched to colours.
The game between
This idea of seeing jersey colour and immediately knowing what team the player belongs to is the opposite of
The inverse function we are looking at identifies the team based on jersey colour. Take a look at the mapping for the function above moving from left to right.
Here we can see that the relation between colour and team is not a function. What would fix this relationship between
Now
Let's look at this mapping relationship in a function machine. Choose a team to pass through the machine. The machine assigns the team to a colour, then reverses the assignment. In other words, the machine applied the function rule then the inverse function rule.
Every time you pass through both machines, you get out the team's
Currency Conversion
International tourism reached over 4 million arrivals each day in 2019. With so much travel between countries, people are more aware of their spending power. That is, how far a
Along your trip, you find many different markets take only cash. To prepare for your next trip to the market, you withdraw cash. The conversion function is
user enters whatever amount they want
to spend on souvenirs, which means you need to withdraw
user must do this calculation and enter the amount +- .5
Take a stroll through the market and decide what you want to buy.
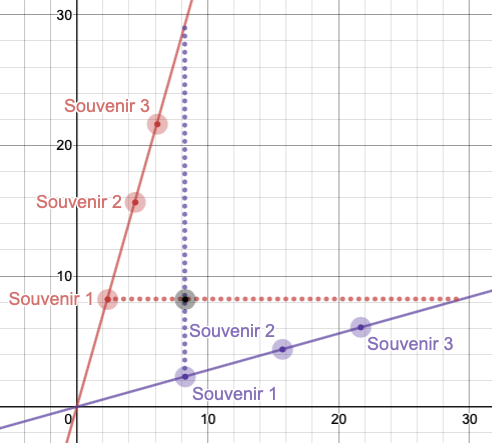
Visual relationship
We can represent this relationship between the cost in
Recall that earlier we used the equation
In fact, the most important difference is that the input and output values are switched. We saw this relationship between functions above in the jersey example. Using this observation, we can see that
The graphs of inverse functions have some interesting features. First, this idea of switching inout and output values helps us plot points for
https://www.desmos.com/calculator/ff6489z9ns
https://www.desmos.com/calculator/tlscgnsyy3
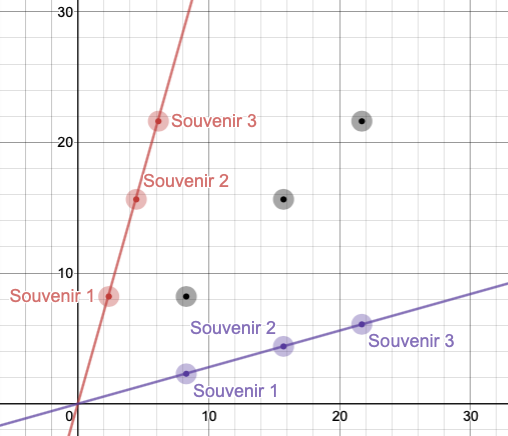
There is another interesting feature of inverse functions, though it may not be immediately obvious. Let's make some measurements between lines to see if the interesting feature emerges.
Begin by measuring the vertical distance from
This distance is the same as the vertical distance you measured! Make the same measurements for each of the souvenir points.
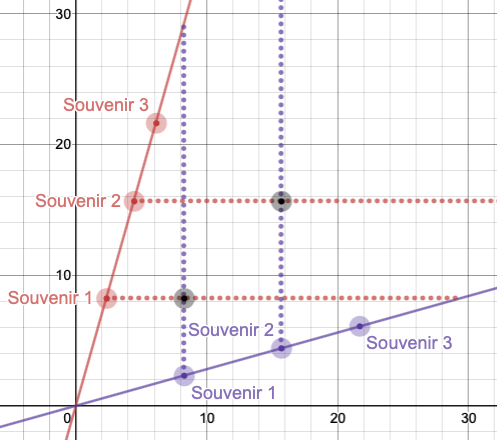
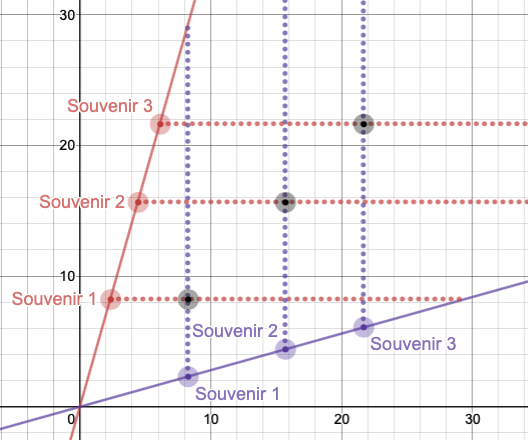
Notice that the intersection points of each of these measurements fall on their own line.
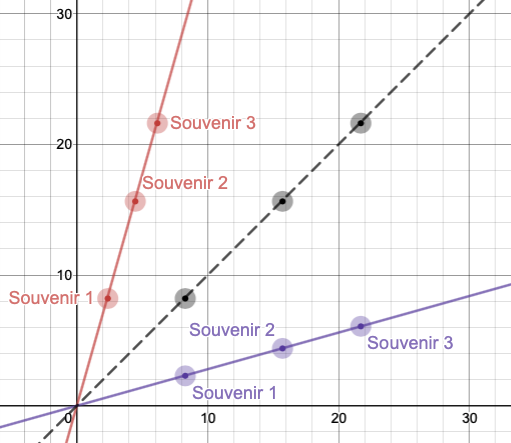
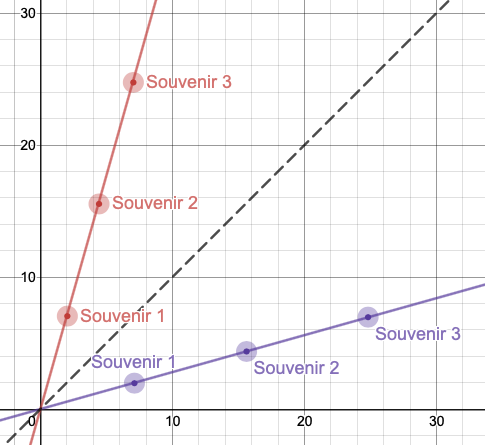
The equation of this line is y=
hide until blank filled
which simplifies to y=x. Notice that if we were to fold the coordinate plane along the line y=x,
In fact, all inverse functions are symmetric over the line y=x. The tools we used to arrive at this observation are the same that we can use to determine whether two functions are inverses. Let's take a closer look at this with a new graph shape called a parabola.
Parabolas
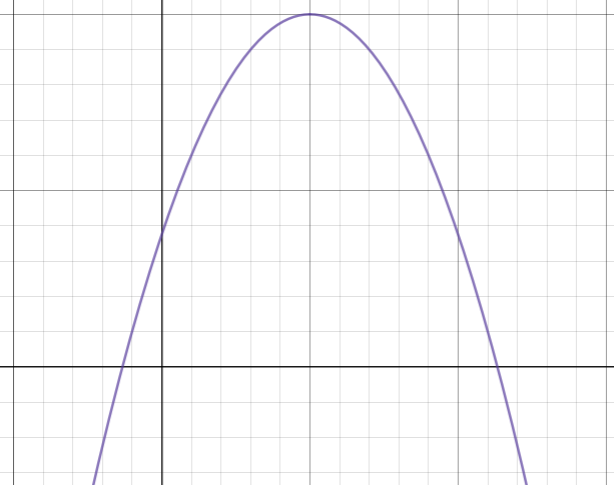
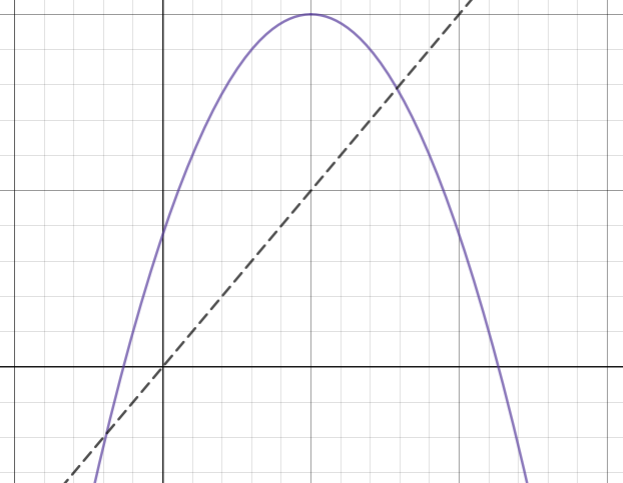
We call this shape a
The parabola passes the vertical line test, so it is a function. We just observed that inverses are symmetric about the line y=x. Make a copy of the parabola and rotate it in the coordinate plane to make it a reflection of the original parabola over the line y=x. Reflection in this case means that the two parabolas are symmetric over y=x.
undefined
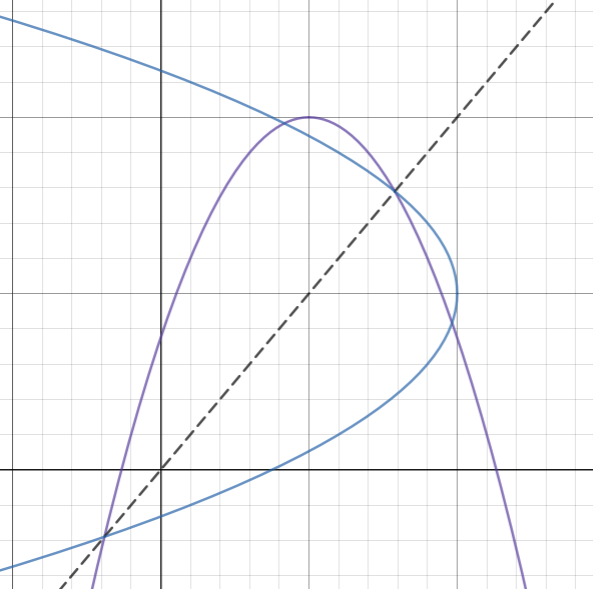
The inverse parabola has the same mirror look as the currency functions. Recall the ordered pairs on those line were switched. That is (
Fill in the table with the coordinate points for each key feature in the original parabola. Verify that their inverses appear on the rotated parabola.
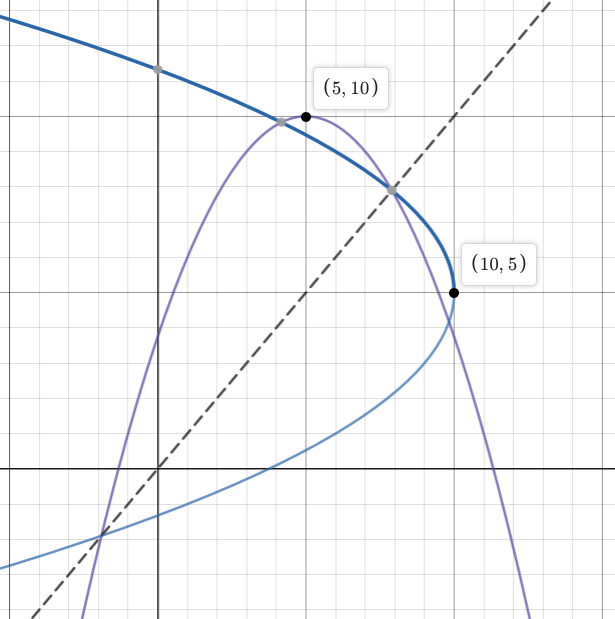
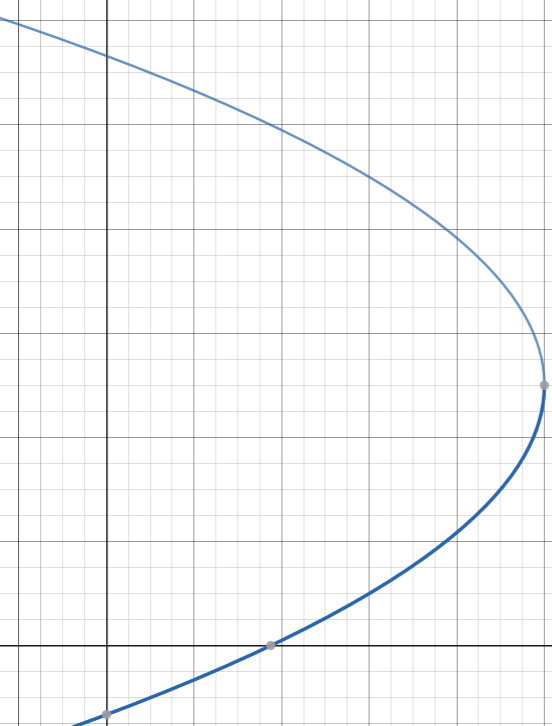
According to the properties of inverses, this is the inverse of the original parabola. It's symmetric over y=x and the points on this curve are the inverses of the points on the original parabola. The last thing we need to do is check that it is a function.
The inverse function doesn’t pass the vertical line test. It isn’t actually a function! When we were looking at the jersey example, we changed the team to colour function so that each team was assign to only one colour. Can you apply that idea here?
undefined
https://www.desmos.com/calculator/ywpamz642r
When we change the
Algebraic Relationship
The Caribbean islands are another popular tourist destination. Their iconic beaches and crystal blue waters paint a picture of relaxation. Bermuda, an island country in the Caribbean, is one of the few places in the world that use both Celsius and Fahrenheit temperature scales in meteorology. Let's set up a hammock in the this shady nook and take a look at the relationship between these temperature scales.
Recall that inverting money from one currency to another are inverse functions. We looked at this using graphs. Let's look at converting temperatures from one scale to another to see if this is indeed an instance of inverse functions.
The forecast calls for a high of 27 degrees Celsius today. We missed the report that included the temperature in Fahrenheit, so we Google the conversion and find C(x)= . Find today's high in Fahrenheit.
undefined
Substitute 27 in for C(X)
Use inverse operation on to move 9
Use inverse operation to move 5
Use inverse operation to move 32
x, representing the temperature in Fahrenheit, is isolated
Today's high in Fahrenheit
This is a familiar process for solving equations. We can use this same process to find inverse functions algebraically. Let's take a look at two key steps in solving the equations above.
Original Function:
Inverse Function:
Recall that we substituted 27 in for C(x) since it was our given temperature. Let's put y in for 27 to represent the output value in an ordered pair.
Original Function
Inverse Function:
Now remember that to graph the inverse function when we were buying souvenirs at the market in , we swapped the x and y coordinates. That is, we switched the input and output. Let's do that same thing in the inverse function.
Recall the notation for inverse functions use the letter name of the original function with a -1 in the exponent location. This means y in the inverse function represents
Take another look at the original and inverse functions side-by-side.
Recall from the jersey example above that passing a value through a function machine then its inverse function machine gives the same value in the end. We called this
Let's determine whether these two functions are inverses.
The function machine indicates that f(x) and g(x)
Let's find the inverse function of f(x).
substitute y in for f(x)
switch x and y
solve for y as usual
$\frac{-2x+8}{3}=y$
substitute
We know have several ways of identifying and verifying inverse functions. Select your favourite method and describe why.
[option 1](inverting equations algebraically) [option 2](graphing using coordinate points and their inverses) [option 3](graphing using y=x as the line of symmetry) [option 4](mapping diagram)
Functions and inverse functions are fundamental ideas in coding and deciphering. Check out Codes and Ciphers to see these ideas in action!
